1. 개요
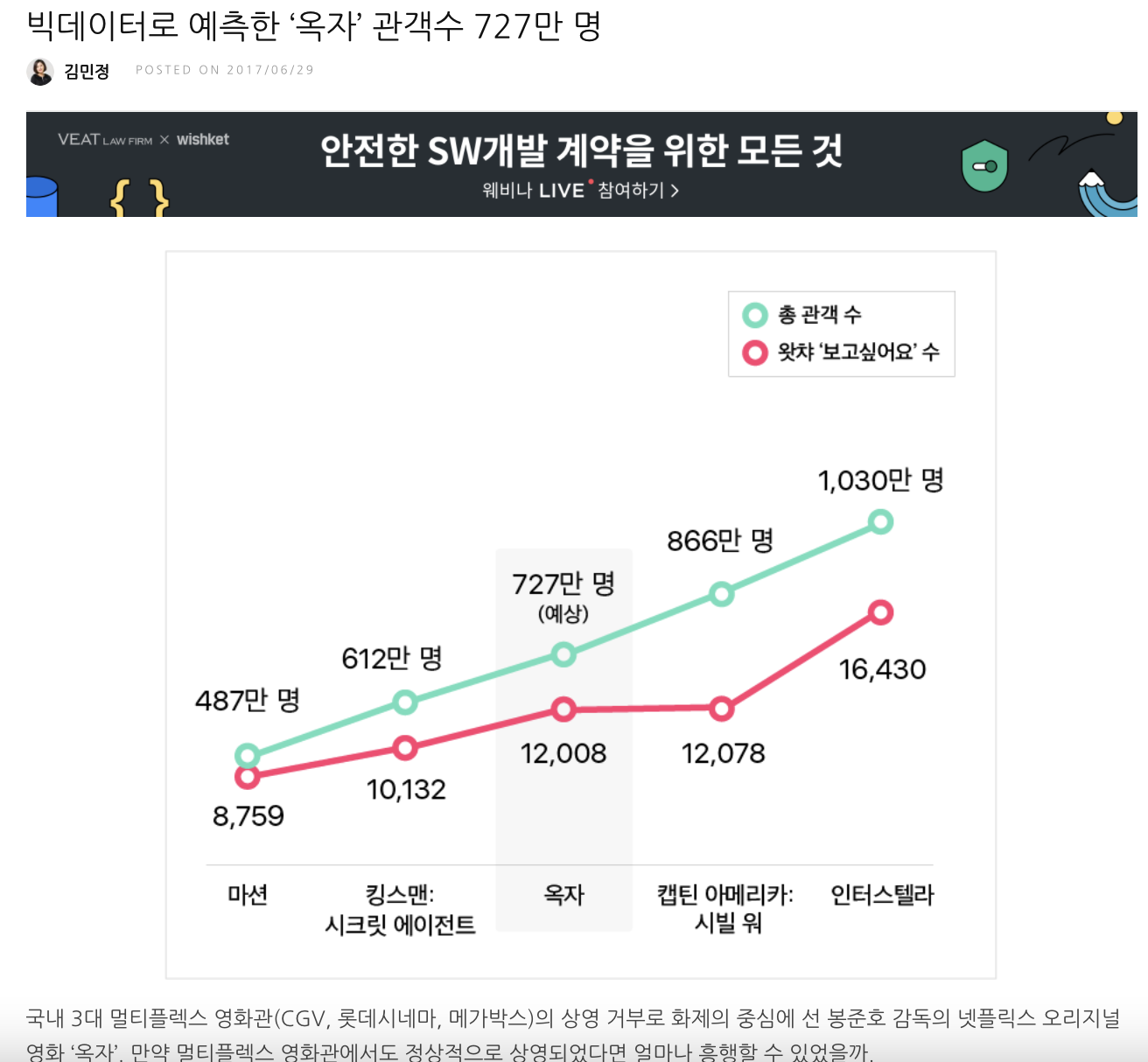
- 2017년에 왓차 ‘보고싶어요’ 수를 기반으로 옥자의 예상 관객수에 관한 내용이 기사화 됨
- 이 기사에 제공된 내용을 실제 Python을 통해 단일 변수에 의한 선형회귀 예측 알고리즘을 작성해 보는 것이 이번 내용의 목표임
2. 준비 사항
2.1 관련 자료 확보
- Google Class에 공유해 둔 수업 “003-선형회귀”에서 watcha-linear-regression.zip을 다운로드
2.2 실습영상 참조
-
Google Class에 공유한 실습영상.mov를 통해 실습을 진행
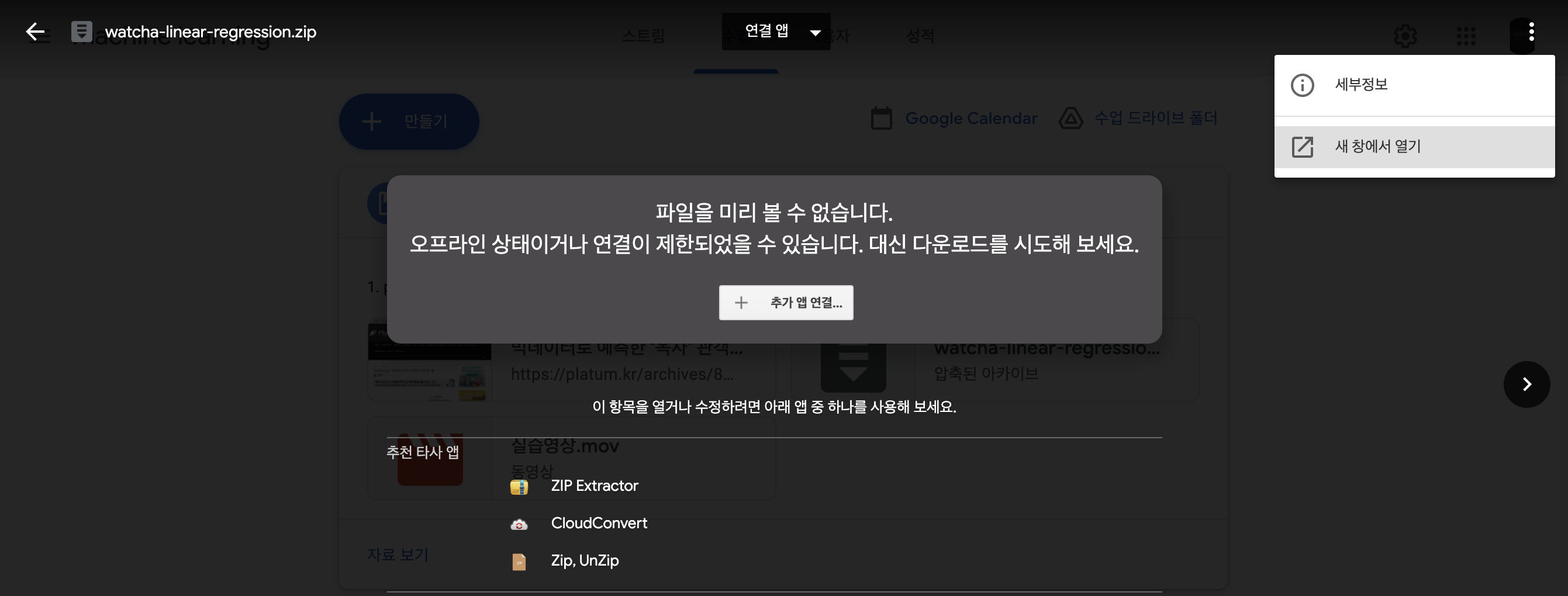
구글 클래스에서 관련 자료 다운로드는 [해당 파일 클릭] > [우측 상단의 “…“클릭] > [새 창에서 열기] 후 다운로드 수행이 필요
-
파일 다운로드 방법 참고
3. 스크립트 내용 해설
- 실습한 스크립트 내용에 대한 이해를 위해 스크립트 구간 별 간단한 설명을 추가함
3.1 필요 라이브러리 설정
-
본 실습을 위해 필요 라이브러리를 설정하는 스크립트
import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline3.2 학습 데이터 가져오기
-
예측 알고리즘을 위한 학습용 데이터를 가져오기
df = pd.read_csv("./watcha.csv") #df는 data frame의 준말로 변수의 이름임 df # 이것은 데이터를 화면에 뿌려 보기 위한 스크립트 -
df의 shape을 통해 몇 by 몇의 행렬인지 확인해 봄
df.shape
3.3 df 데이터에서 x값만 추출하기
- df는 키:값 형태로 데이터를 저장하고 있는데 “X”라는 키를 통해 해당 키에 관련된 데이터를 추출
- 추출된 데이터는 차후 연산을 위해 4x1 행렬로 reshape 함
raw_X = df["X"].values.reshape(-1,1) raw_X.shape, raw_X
3.4 df 데이터에서 y값만 추출하기
- “Y” 키값을 통해 관련된 데이터를 추출
y = df["Y"].values y.shape, y3.5 학습 데이터 그래프 출력하기
- matplotlib를 통해 추출된 학습 데이터 X값과 Y값으로 그래프 출력
plt.figure(figsize=(10,5)) plt.plot(raw_X,y, 'x', alpha=0.5)
3.6 X 매트릭스 구조 변경
- X값을 전부 1로만 되어 있는 매트릭스와 결합하여 2행4열의 매트릭스로 구조를 변경함
X = np.concatenate( (np.ones((len(raw_X),1)), raw_X ), axis=1) X[:5]
3.7 초기 선형 함수 도출
- 지금까지 x값과 y값을 토대로 y = w1*x + w0 형태의 선형함수를 도출
-
도출된 선형 함수를 그래프로 표출하여 실제 학습값과의 차이를 확인 함
w = np.random.normal((2,1)) #임의의 w1, w0 값 할당 w.shape, w #값을 표출하여 할당된 값 확인 y_predict = np.dot(X,w) #w1*x + w0 연산 수행 y_predict.shape, y_predict # 연산된 값을 그래프로 표출 plt.figure(figsize=(10,5)) plt.plot(raw_X,y,"o", alpha=0.5) plt.plot(raw_X,y_predict) plt.show()4. 가설함수 작성
- 비용함수를 통해 수정된 w1,w0값으로 w1*x + w0 함수를 다시 도출하는 역할 수행
#함수 정의 def hypothesis_function(X, theta): return X.dot(theta)의 #함수 연산 h = hypothesis_function(X, w)
5. 비용함수 작성
- 실제 y값과 가설함수 w1*x + w0의 결과값 사이의 차이를 확인하는 함수 작성
def cost_function(h, y): return (1/(2*len(y))) * np.sum((h-y)**2) c = cost_function(h, y)
6. 경사하강법 작성
- 실제 y값과 가설함수 w1*x + w0의 결과값 사이의 차이를 최소화할 수 있는 w1과 w0값을 찾는 방법중에 하나인 경사하강법을 작성함
def gradient_descent(X, y, w, alpha, iterations): theta = w m = len(y) theta_list = [theta.tolist()] cost = cost_function(hypothesis_function(X, theta), y) cost_list = [cost] for i in range(iterations): t0 = theta[0] - (alpha / m) * np.sum(np.dot(X, theta) - y) t1 = theta[1] - (alpha / m) * np.sum((np.dot(X, theta) - y) * X[:,1]) theta = np.array([t0, t1]) if i % 100== 0: theta_list.append(theta.tolist()) cost = cost_function(hypothesis_function(X, theta), y) cost_list.append(cost) return theta, theta_list, cost_list
7. 학습 수행
- 지금까지 도출된 학습데이터, 가설함수, 비용함수, 경사하강법을 이용하여 학습 수행
- 학습은 iterations 값을 통해 반복할 횟수를 결정
- alpha값을 통해 learning rate 즉, w1*x + w0 에서 w1과 w0간의 변화 수준을 얼마나 가져갈지 정함
iterations = 100000 alpha = 0.0000000001 theta, theta_list, cost_list = gradient_descent(X, y, w, alpha, iterations) cost = cost_function(hypothesis_function(X, theta), y) print("theta:", theta) print('cost:', cost_function(hypothesis_function(X, theta), y))8. 예측 수행
- 학습을 통해 도출된 w1*x + w0 함수를 통해 최종적으로 왓차에서 영화 ‘옥자’의 보고싶어요 값인 12,078명의 값을 통해 총 관객수를 예측함
test_x = np.array([1, 12078]) h = hypothesis_function(test_x, theta) h #약 768.097 도출 - 뉴스에서 예측한 727만명과 유사한 768만명의 예측값을 도출함



댓글남기기